Doppler Shift
多普勒效应
1842年奥地利物理学家克里斯琴$\cdot$约翰$\cdot$多普勒(Christian Johann Doppler)发现一种有趣的物理现象:当声源与声波接收器处于相对运动状态时,声波接收器接收到的声源频率不同于声源发射的频率,且频率的变化与二者的相对运动速度有关。后来人们发现不止是声源,其他信号源和观察者的相对运动都会导致观察者接收到的信号频率发生变化,于是为了纪念多普勒的这一发现,这一类现象就被称作多普勒效应(doppler effect)。
| The doppler effect is the change in frequency or wavelength of a wave in relation to observer who is moving relative to the wave source. |
多普勒频移
无论是信号源运动、还是观察者运动或者两者都运动,本质上都没有区别,在这里我们假设信号源是静止的,观察者是运动的,并且所有的测量都是在信号源的参照系中进行的,这样不失一般性,因此有以下两种情况:
观察者靠近信号源,连续波之间的到达时间降低,频率增加;
观察者远离信号源,连续波之间的到达时间增加,频率降低。
观察者接收到的频率与信号源发射出的频率之间频率的改变量被称作多普勒频移(doppler shift)。
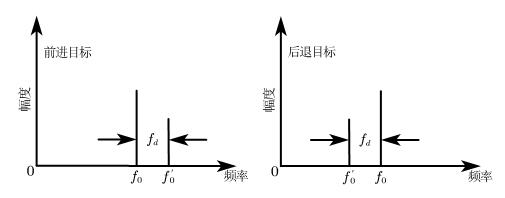
一般雷达系统中的多普勒频移
针对雷达系统(电磁波传播速度为$c$),设雷达的固有频率为$f_0$,其固有波长为$\lambda_0$。
目标靠近雷达
如下图所示,考虑一个宽度为$T_r$(s)的脉冲入射到一个一速度$v$向雷达运动的目标上:
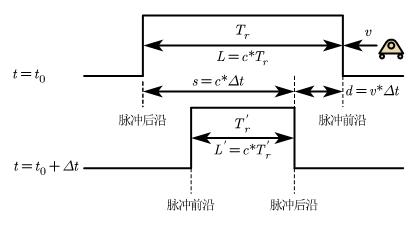
定义$d$为在间隔$\Delta t$内目标的运动距离:
其中,$\Delta t$等于从脉冲前沿碰到目标到脉冲后沿碰到目标之间的时间。
定义$s$为在间隔$\Delta t$内脉冲前沿和脉冲后沿的运动距离:
那么入射脉冲宽度$T_r$为:
反射脉冲宽度为:
可以建立入射脉冲宽度$T_r$和反射脉冲宽度之间的如下关系式:
由于脉冲宽度$T_r$与脉冲重复间隔$PRI$成正比,脉冲重复频率$PRF$与脉冲重复间隔$PRI$成反比,故:
然而,由于周期数不变,反射信号的频率会升高相同的因子1:
1. 实际上,因子$(c+v)/(c-v)$通常称为时间膨胀因子。 ↩
则多普勒频移为:
但是因为$v\ll c$和$c=\lambda_0f_0$,所以:
目标远离雷达
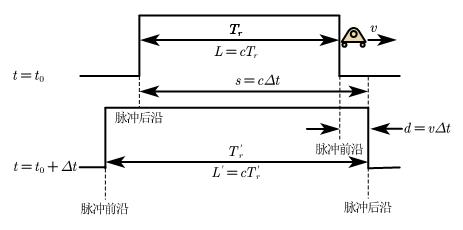
分析同上,则多普勒频移为:
拓展到一般情况
当雷达与目标不是径向运动且雷达和目标都有运动时,设目标的速度为$v_d$,方向与目标雷达连线之间的夹角为$\theta_d$,设雷达的速度为$v_s$,方向与目标雷达连线之间的夹角为$\theta_s$,则可得到经典多普勒频移普适公式:
合成孔径雷达系统中的多普勒频移
由于雷达与目标的相对运动,接收信号经历了多普勒频移,这一多普勒频移存在于解调后的接收信号中,与脉冲带宽相比,频移很小,难以察觉,但是当沿方位向观测时,多普勒频移就很明显了。如下图所示,展示了合成孔径雷达系统中雷达位置和波束在地面覆盖区的简单几何模型以及雷达数据获取的几何关系:
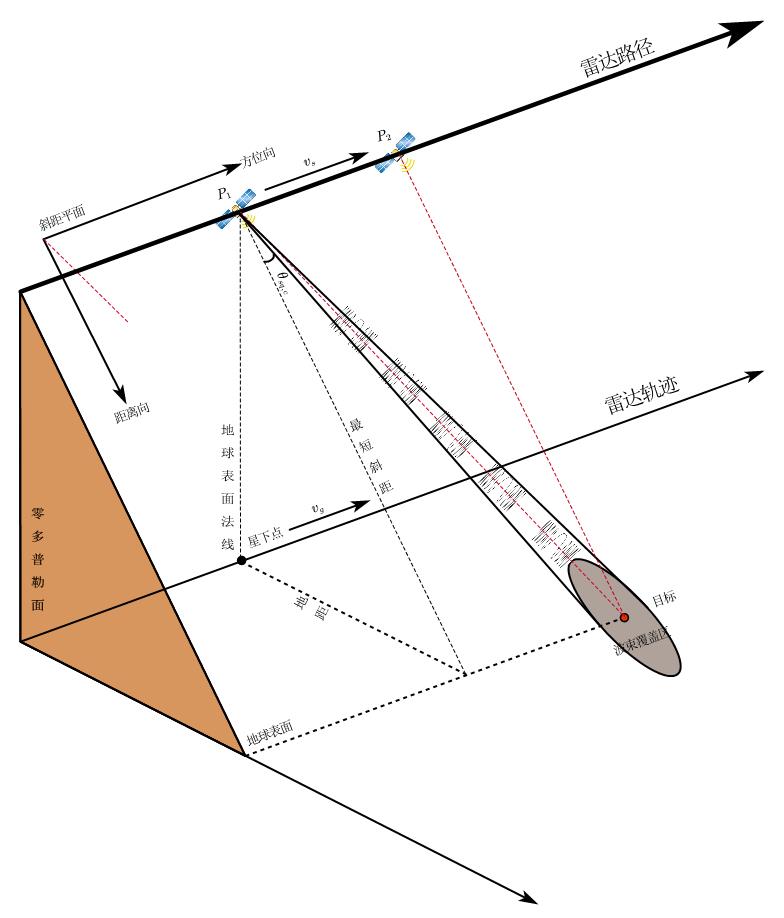
多普勒中心频率
通常SAR数据在方位频域进行处理,则波束中心穿越时刻(2)等效转换为频域中的多普勒中心频率()。
2. 雷达最接近目标的位置称为最近位置,对于单个点目标,为了便于分析,起始时刻通常选在最近位置时刻,也称零多普勒时刻。雷达波束中心经过目标的时刻称为波束中心穿越时刻,记为。当波束前视时,为负,当波束前视时,为正。 ↩
2. 容易推导: ↩
根据经典多普勒频移普适公式,我们可以很容易地得到多普勒中心频率:
同时,我们知道$\eta=\eta_c$处的多普勒中心频率正比于瞬时斜距$R(\eta)$3的变化率(即径向速度):
3. 双曲线模型:$R(\eta)=\sqrt{R_0^2+v_r^2\eta^2}$ ↩
3. 抛物线模型:$R(\eta)=R_0+\frac{v_r^2\eta^2}{2R_0}$ ↩
可见,两种推导思路的结果是一致的。
多普勒带宽
多普勒带宽是目标在雷达3dB波束照射期间产生的频率漂移,如下图所示:
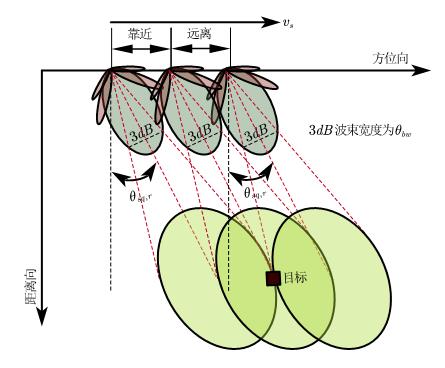
当雷达左侧3dB波束边缘照射目标到雷达波束中心照射目标,雷达是靠近目标的,此时由于雷达与目标之间的相对运动产生的多普勒频移为:
当雷达波束中心照射目标到雷达右侧3dB波束边缘照射目标,雷达是靠近目标的,此时由于雷达与目标之间的相对运动产生的多普勒频移为:
则多普勒带宽为:
由于3dB波束宽度较小,可利用以下近似,则有:
这一带宽决定了采样要求,即确定了PRF的下限。然而,在处的波束边沿,信号强度只下降了6dB,并且方位谱衰减得比较慢,因此过采样率一般应该取,以减小方位模糊功率。
方位混叠与多普勒中心
持续更新中…
本文作者水平有限,如有错误,恳请批评指正!
