White Guassion Noise
高斯白噪声生成函数
高斯白噪声的概率密度服从高斯分布,即正态分布:
其中有$\mu$(平均值)和$\sigma$(标准差)两个参数。
如果一个噪声,它的幅度分布服从高斯分布,而它的功率谱密度又是均匀分布的,则称它为高斯白噪声。
下面介绍MATLAB中生成高斯白噪声的三种方法:
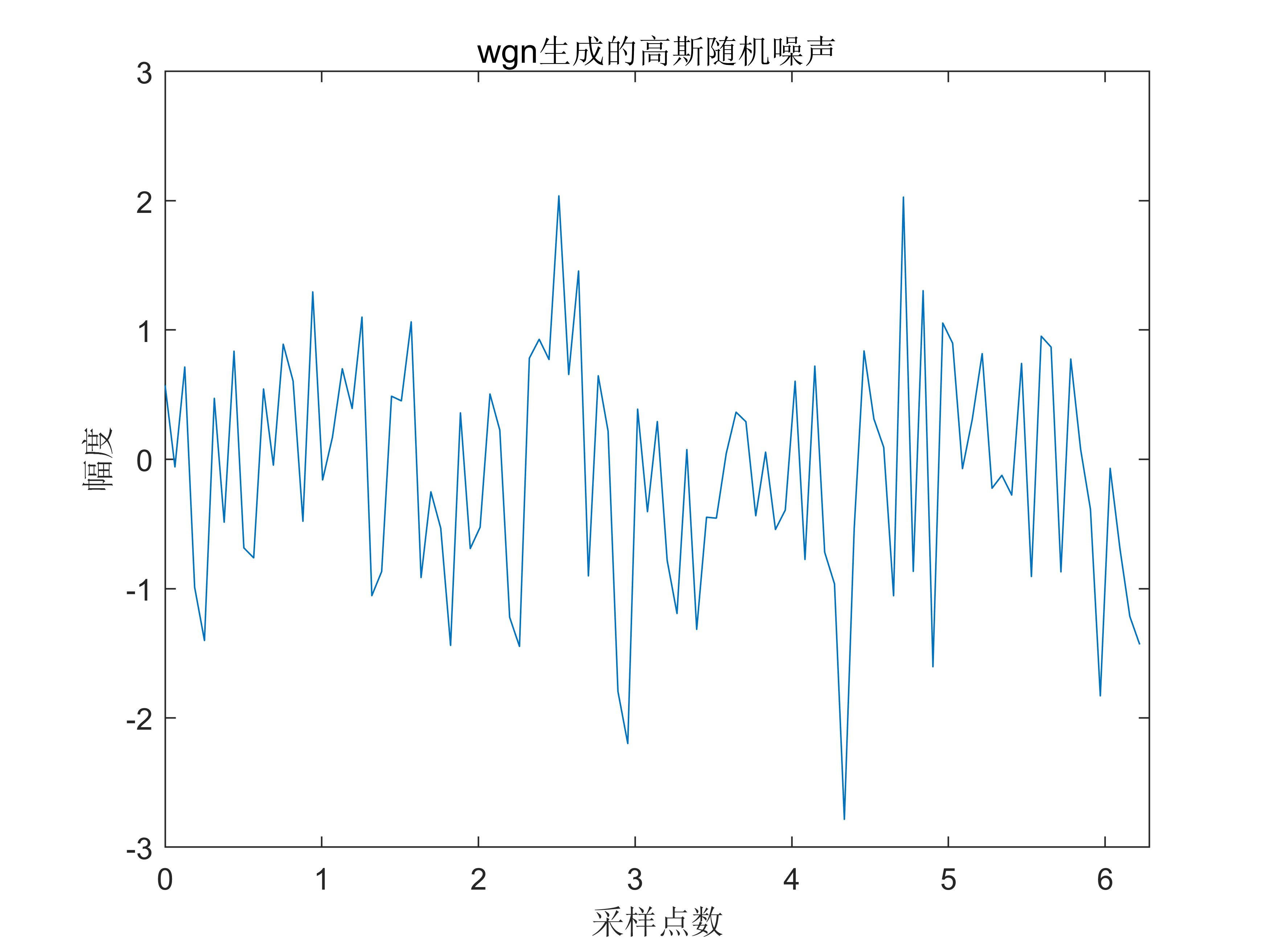
wgn
noise = wgn(m,n,power) |
产生m行n列的高斯白噪声矩阵,power为以dBW为单位的指定输出噪声强度。
0dBW=10lg(P/1W)=10lg(1W)=10lg(1000mW)=10lg(P/1mW)=30dBm
x = 1:1:1000; |
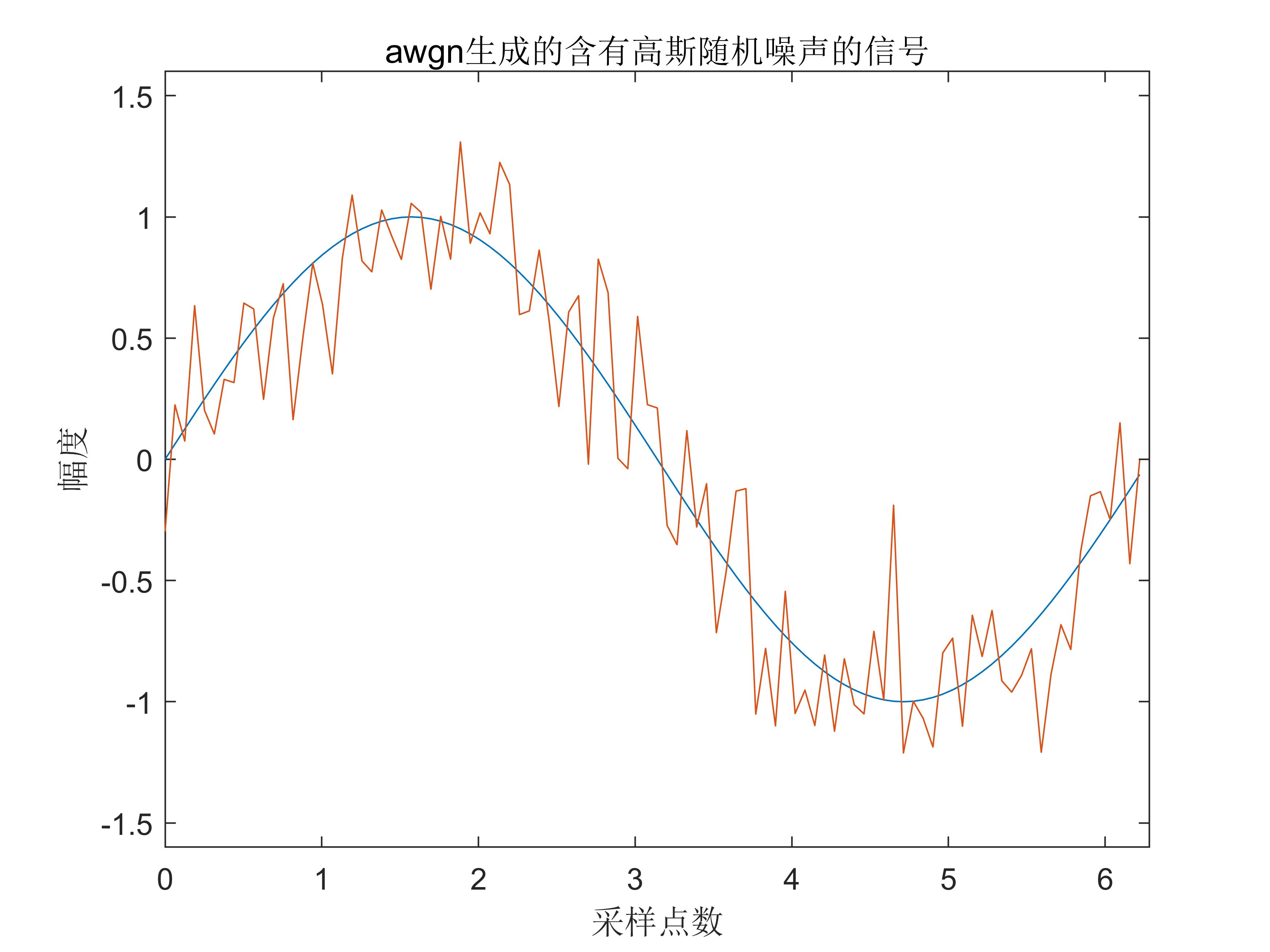
awgn
noise = awgn(st,SNR,'measured') |
在某一信号St中加入高斯白噪声,高斯白噪声的的维度与信号st的维度一致。
awgn(st,10)是假设信号st的功率为0dBW,然后添加噪声,使得SNR=10;
awgn(st,SNR,’measured’)是先测量信号st的功率,然后添加噪声,使得SNR=10;
x = (0:2*pi/100:2*pi-2*pi/100)'; |
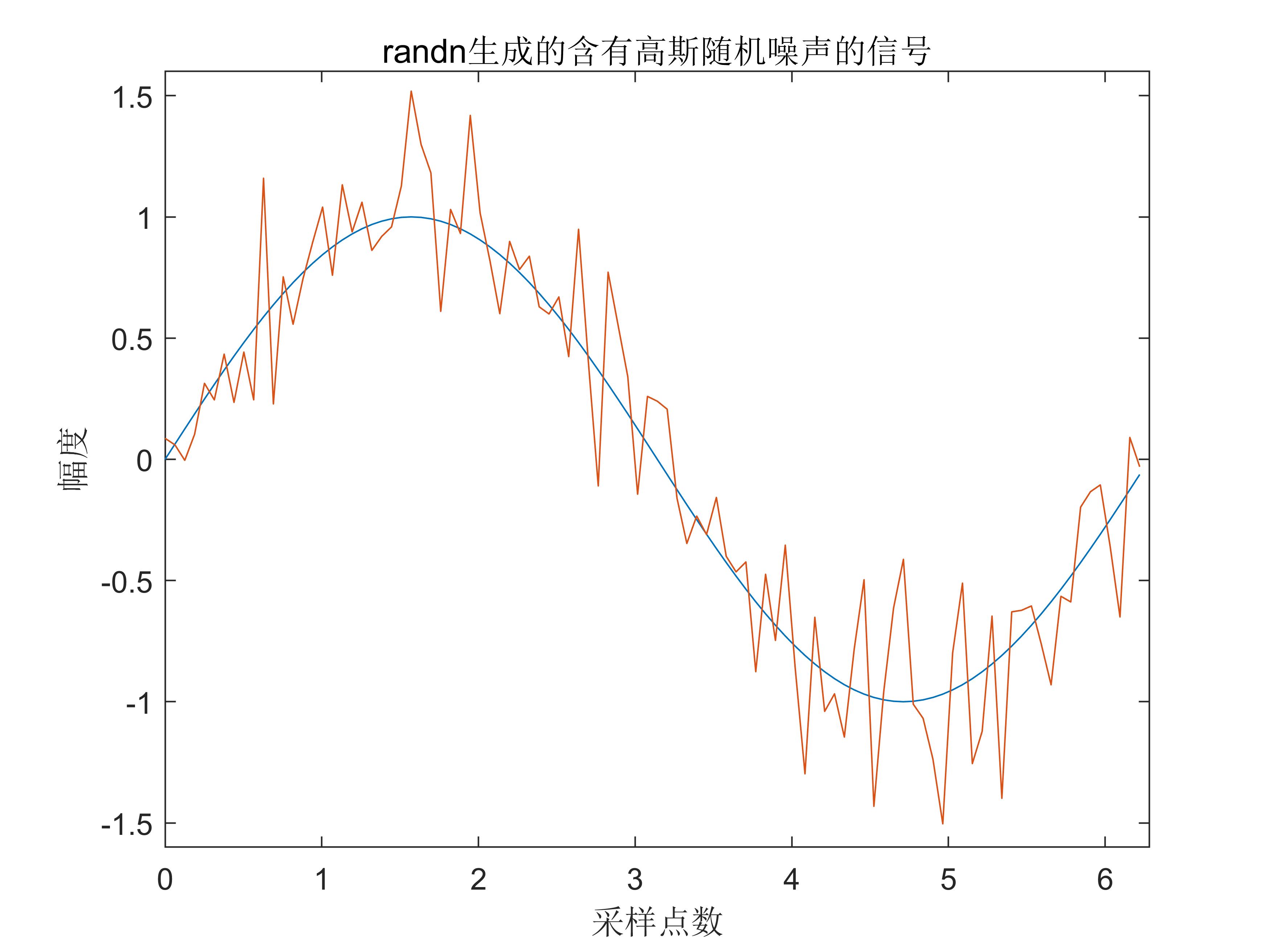
randn
noise = mu + sigma*randn(m,n) |
产生m行n列的高斯白噪声矩阵,$\mu$为其均值,$\sigma$为其标准差。
如果要在某一信号st中加入高斯白噪声,一般将信号st作为高斯白噪声的均值。
x = (0:2*pi/100:2*pi-2*pi/100)'; |
本文作者水平有限,如有错误,恳请批评指正!
此文章版权归Henry Wang所有,如有转载,请注明来自原作者
评论
